Course Description
This course gives an introduction to analysis, and the goal is twofold:
1. To learn how to prove mathematical theorems in analysis and how to write proofs.
2. To prove theorems in calculus in a rigorous way.
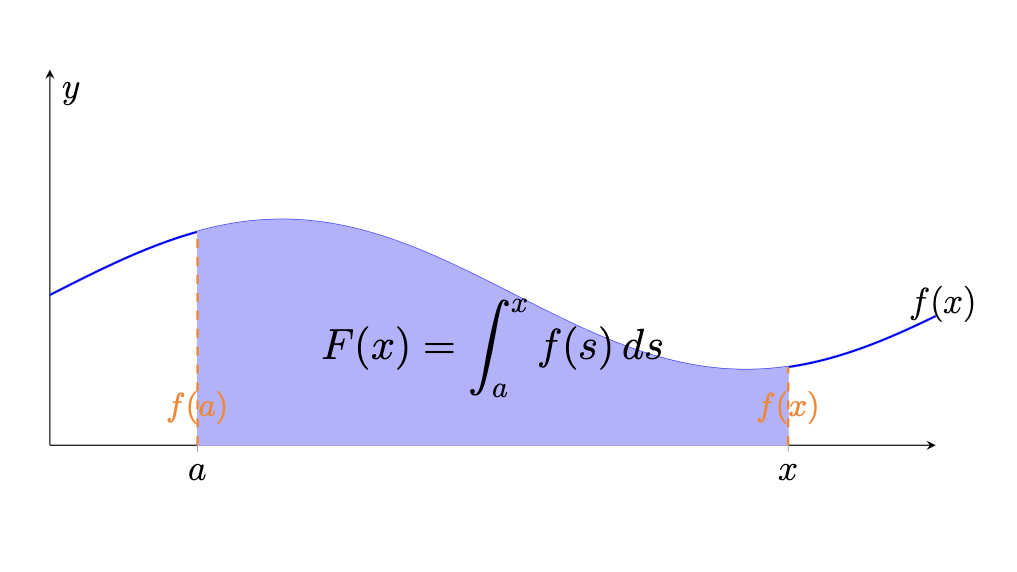
The course will start with real numbers, limits, convergence, series and continuity. We …
This course gives an introduction to analysis, and the goal is twofold:
1. To learn how to prove mathematical theorems in analysis and how to write proofs.
2. To prove theorems in calculus in a rigorous way.
The course will start with real numbers, limits, convergence, series and continuity. We will continue on with metric spaces, differentiation and Riemann integrals. After that, we will move on to differential equations.
Course Info
Instructor
Departments
Learning Resource Types